For very large floating point
(decimal) values, we can use Scientific
Notation.
For example, in Chemistry a Mole is defined as 6.02 x 1023
molecules.
We could write this as: 6.02*10*10*10
.... 10 , repeating 23 tens.
But it's simpler to write: 6.02e23
.
The number 6.02 is called the mantissa.
The number 23 is the exponent.
We can also do arithmetic with these Scientific Notation numbers.
For example: 6.02e23 * 2
==> 12.04e23
But Java will always normalize
the result, writing the mantissa
so that it has
just one number before the decimal point. Then the exponent
must also change.
So: 12.04e23 ==>
1.204e24.
You might not need to use such big numbers, but you might be surprised
when
Java uses Scientific Notation to print a result.
For example : 1000.00 * 1000 *
1000 * 1000 ==> 1.0e12
It's easy to change the Scientific Notation back to a normal number.
The exponent 12 tells us
to move the decimal point 12 spots to the right.
That means you need to add some zeroes.
1.0e12 ==> 1 000 000 000 000
= 1 trillion
Scientific notation is the most general representation for a float (floating point) value.
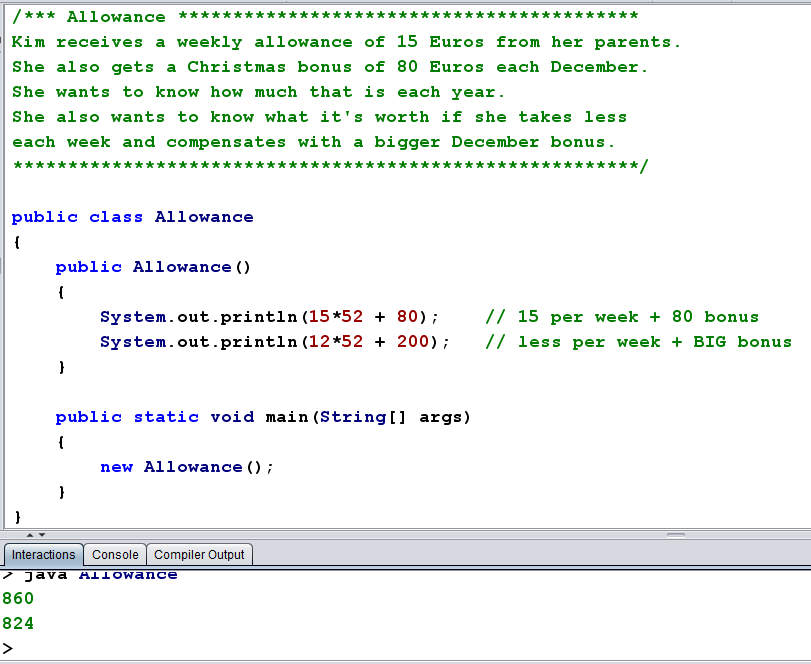
Investigation
Explanation
Java float values only have 8
decimal place accuracy. So when something like
6/11 is stored, it can be stored as 0.54545454. There should
be lots more repetitions of 54,
but there is no space and the rest is truncated (chopped off). Or it might get rounded
off,
which makes it closer to being correct, but still not 100% correct.
In fact, the actual value
produced by 6/11.0 is 0.54545456, which isn't even rounded off
correctly. Once the number
is stored in the memory, the storage error is permanent. In a long
calculation,
the truncation errors will occur after each part of the calculation,
and may result in a noticeably incorrect answer. But if you are
lucky,
rounding errors in one part of the calculation may balance out with
truncation
errors in another part, and produce a very accurate answer at the end.