Solving Equations

  Download Source Code



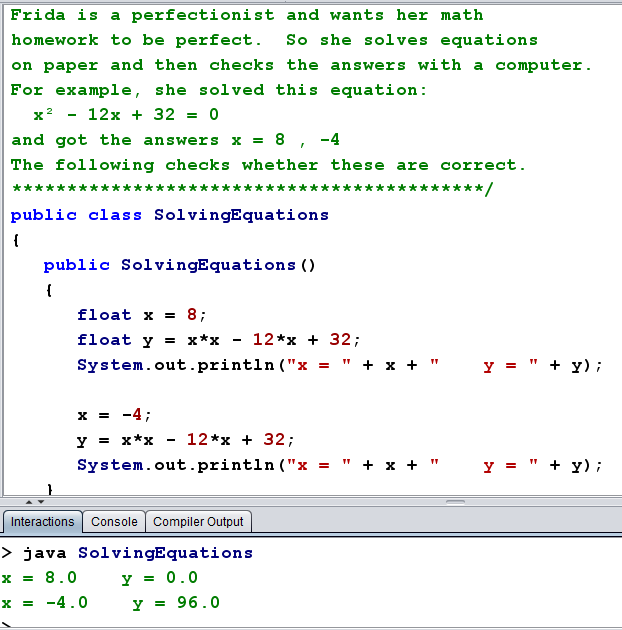
So it looks like Frida's answer x = -4.0  is incorrect, while x = 8.0  is correct.

Guess and Check

In math class, you learned to "solve" equations by doing algebra.  Algebra is complex and difficult and
requires clever thinking skills to do correctly.  Computers are certainly not "clever".  Computers do things
by following specific commands, not by "thinking" and certainly not by doing algebra (well, there
actually are artificial intelligence systems that can do algebra, but these are not very common).

Computers ARE good at performing calculations quickly and accurately.  Combined with human
cleverness, they can be used to solved difficult problems, even problems involving very large numbers
and complex calculations.

A common method for solving problems is GUESS and CHECK.  The human tries to guess the
answer, and the computer checks whether the guess was correct or not.  In the example program above,
the numbers 8 and -4 weren't actually "guesses", but they were the result of some algebra.
Still, the computer did the calculations to check the answers, and one of them was wrong.

Consider a more difficult problem - find a number X so that  2X - X = 100 .
We could guess X = 7, which gives   27 - 7 =  128 - 7 = 121.  So we would try a smaller number.
Here is a program that makes guessing and checking quicker.

float x = 7;

println( Math.pow(2,x) - x );
Try it
Run this program and try to guess the correct value for X .  You can stop when you have 2 decimal places.


Practice

For each problem, write a program and use guess and check to find solutions.
In each case, you can stop when you have 3 significant figure accuracy (e.g. 375 or 1.23 or 0.000789).
  1. Solve :  x3 - 5x - 10 = 0
     
  2. Find numbers A and B so that :  A*B = 20  and  A-B = 5
     
  3. Solve:  x + x2 + x3 + x4 = 1000000 

Computational Thinking

When we create a program to represent a problem, we call it a computational model.
The process of creating computational models is called computational thinking.
The important issue is to find commands that represent the problem accurately.
That includes both the data (variables and values) and algorithms (calculations).

Mathematics problems are pretty easy to model, because they already contain numbers and
variables and formulas.  "Real world" problems are generally more complex, involving more
than simple mathematical formulae.  Computational Thinking means to analyze the problem
in a way that makes it possible to produce a computer program that models the problem,
and which a computer can implement automatically.

You don't know enough Java commands yet and so you can't model very complex problems,
but here is one that you can try.  It's a physics problem.