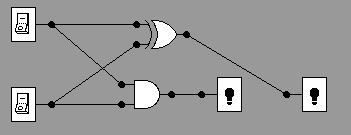
Half Adder and Full Adder Circuits

-- Half Adder --

A half-adder circuit adds 2 bits (input) and gives a 2 bit answer (output).  Here is the truth-table :

    Inputs          Outputs

Looking at the output columns, we see that

• C has the same logic as an AND gate 
• D has the same logic as an XOR gate.

So we conclude that the following circuit will work:

                                                     Carry              D

This is called a half-adder because it isn't complete.  It would only work
for adding the LSB (least significant bits) of two integers.

-- Full Adder --

For the rest of the bits, there might be a CARRY from the previous place.
That means we need a circuit that can add 3 bits and produce a 2-bit answer.
This is called a full adder:

  <-----  3  inputs ----------> <--- 2 outputs --->

This can be done without a Karnaugh Map by looking for patterns.

The grey section looks like an AND gate  -->   not A and (B and C)
The yellow section looks like an OR gate -->      A and (B or C)
The blue section looks like an XOR gate -->   not A and (B xor C)
The green section is the opposite of XOR -->      A and not(B xor C)

Combining these, we get:     

      X  =    notA and (B and C)  OR   A and (B or C)  

      Y  =    not A and (B xor C)  OR   A and not(B xor C)  

Using these observations, we can build the following circuit:

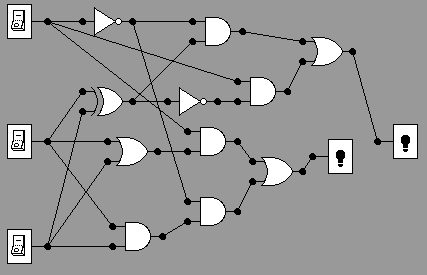
This is too complex.  We'd like something simpler.  A Karnaugh map isn't much help.

The real reason that a half-adder got it's name is that we can use two half adders
plus an OR gate to make a full adder, like this:

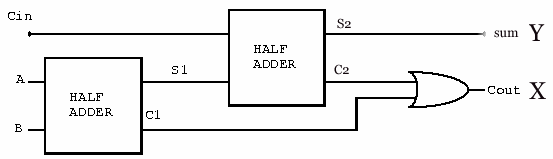
This can be created using an XOR and AND for each half-adder, like this:

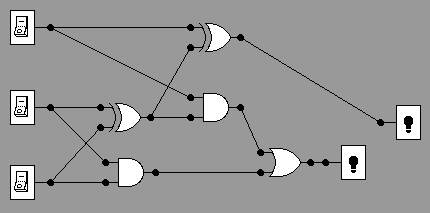
You should memorize the circuit for half-adder, and this circuit which
uses two half-adders to make a full-adder.

-- Register Arithmetic --

A CPU contains several single memory locations called registers.
Addition involves adding 2 registers, 1 bit at a time, to produce an answer in a 3rd register.
At each bit position, a full-adder is used, and it's carry output is copied into
the input of the next full-adder, like this:

This is a 3-bit ripple adder with a full adder at each bit position.