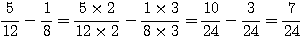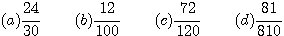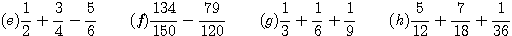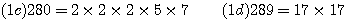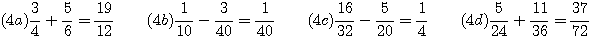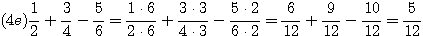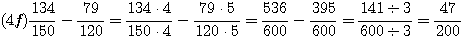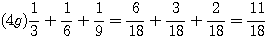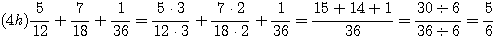Using Factors

Prime Factor Tree

Use a factor tree to break a number down until you reach prime numbers - those cannot be broken down further.

Circle the prime numbers (the ones at the ends), then write them all down to see the prime factorization of the number.

              180       Prime Factorization
           /         \
       10             18
     /      \         /      \
  ( 2 )  ( 5 )  ( 3 )      6
                             /     \
                         ( 2 )   ( 3 )

 So : 180 =  2 x 5 x 3 x 2 x 3

Reducing Fractions

To reduce a fraction:
-  find the prime factorization of the top
-  find the prime factorization of the bottom
-  cross out matching prime factors
-  multiply the remaining primes

Check :  Cross-multiply to get equal numbers

Reduce :   

           2 x 3 x 3 x 5             5           5
=  覧覧覧覧  =  覧  =   覧
     2 x 2 x 3 x 3 x 7         2 x 7       14

Check: 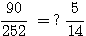       14x90 =? 5x252

                                              1260 = 1260 ｩ

Highest Common Factor  (HCF)

Factors that work in both numbers are called common factors.  The HIGHEST Common Factor (HCF) is the product of all the common prime factors.  But if you can guess the HCF, then you can reduce a fraction without doing the prime factorization.

Reduce : 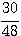   ==>  HCF is 6

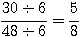         is the reduced fraction.

Least Common Multiple  (LCM)

The Least Common Multiple is useful for adding and subtracting fractions.  If you can get the HCF of 2 numbers, then use the trick shown here to get the LCM.

Finding LCM of 18 and 30

                  6       HCF                   
                /    \
         x3  /      \  x 5
              /        \                   
           18        30
              \        /
        x 5  \      /  x 3           
                \    /
                 90    LCM   90 = 18 x 5 = 30 x 3
                

Adding and Subtracting Fractions

To add or subtract fractions, find a common denominator.  This is the same as a common multiple.  Use the LCM if you can, to keep the numbers small.   Then add (or subtract) the numerators (tops) together and keep the denominators (bottoms) the same.  Then reduce the answer if you can.

If you don't want to think about the LCM, you can always multiply the dentominators to get a common multiple, but this produces large numbers, and you will probably need to reduce the answer at the end.  And be careful with your arithmetic on those big numbers.

Add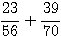  

HCF = 14,   56 = 14 x 4 , 70 = 14 x 5
so  LCM  =  4 x 70 = 5 x 56 = 280

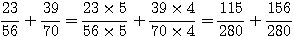
Subtract 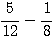   HCF = 4, so LCM = 24

Practice - Show all your work as described in the instructions.
Some ANSWERS are shown at the bottom.  Or use your calculator to check your answers.
In either case, you must still SHOW ALL YOUR WORK.

(1)  Find the prime factorization of each of the following by making a factor tree.
      Check by multiplying the prime factors to get the original number.
     (a)  80              (b)  150            (c)  280           (d) 289

(2)  Reduce each fraction by writing the prime factorization of both numbers, then crossing
      out common factors.  Check by cross-multiplying.
     

(3)  Find the HCF and the LCM of each pair of numbers.  Make a diamond chart as shown above.
     (a)  16 and 20       (b)  20 and 30      (c) 48 and 100    (d)  24 and 720

(4)  Add or subtract the fractions.  Show all your working (as shown in the examples above).
    If you can guess the LCM, that's fine, but you must still show how you multiplied top and
    bottom of each fraction to convert to the LCM.

All answers.  Please note that the students must show their work.  The answers are printed here in abbreviated form for convenience and to make them fit on the web-page.  The last 4 problems have been worked out completely, but students should NOT write their answers this way.  They should write them on several lines under each other.,

   

(3a) For 16 and 20, HCF = 4, LCM = 80     (3b) For 20 and 30, HCF = 10, LCM = 60
                     (3c) For 48 and 100, HCF = 4 , LCM = 1200    (3d) For 24 and 720, HCF = 24, LCM =720